Math AST: Parser in JavaScript

In terms of writing math expressions, there are three forms:

• infix form - the one we get used to 2 * x + 3
• postfix form - 2 x * 3 +
• prefix form - + 3 * x 2.

Form of the expression provides us with the information to interpret it correctly: precedence & associativity. While infix form is very convenient for humans, computers find it ambiguous. Postfix notation (RPN) or abstract syntax trees (AST) is much easier to operate with. That's where parsers come into play.

Parser constructs abstract syntax tree out of tokens - central data structure for all post-parsing activities. Having abstract syntax tree opens new possibilities: simplifying & evaluating math expressions.

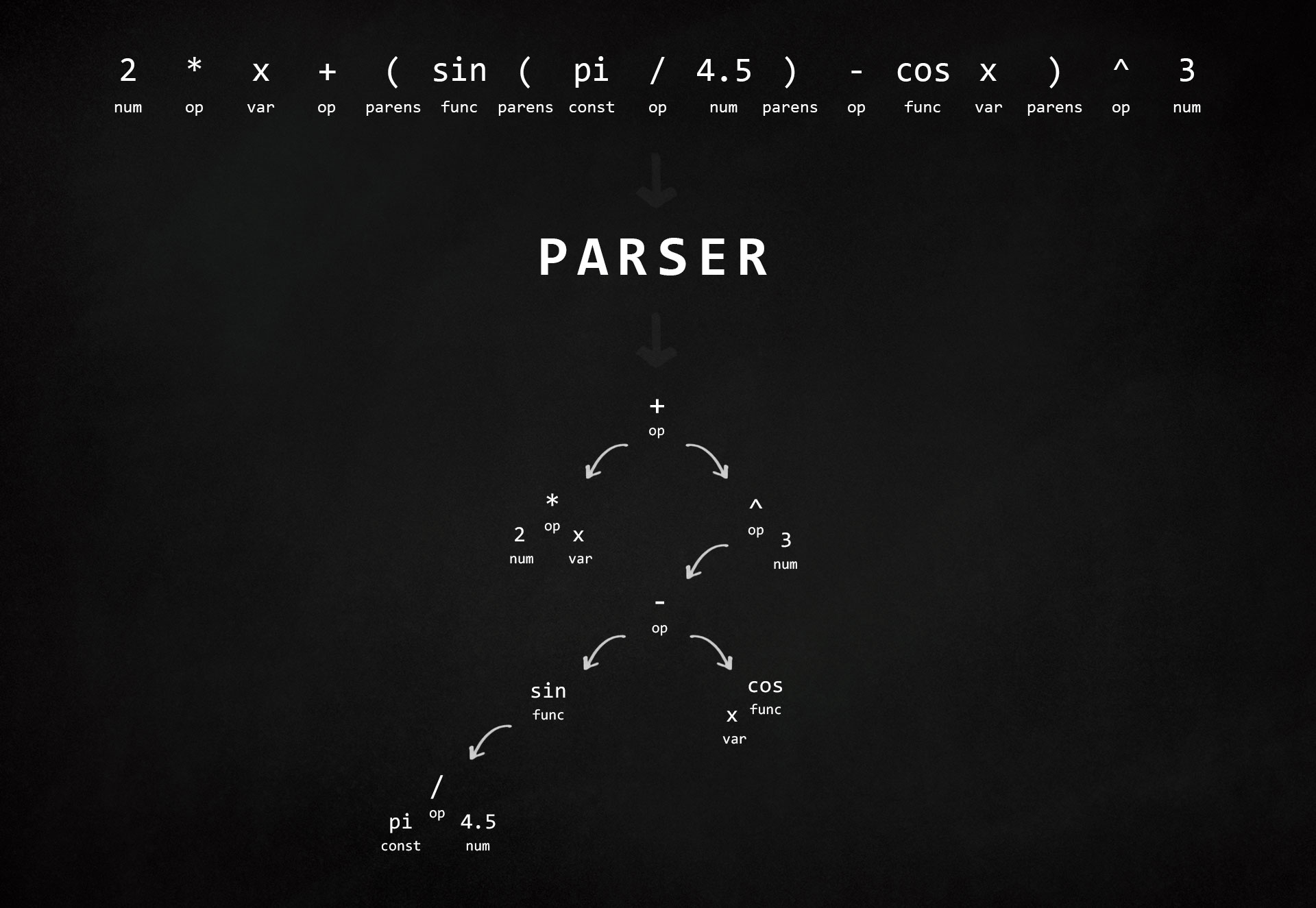
We'll need to split math expression into tokens first, luckly that's what we've already done in the first article.

First of all we will need to augment the config we've used in the first article, to contain the information about operator's precedence & number of arguments.

import types from "./types";

const config = {
  rules: [
    {
      key: "sin|cos|tg|ctg|log|sqrt",
      data: {
        type: types.NAMED_FUNCTION,
        args: 1,
        precedence: 4,
        isLeftAssociative: true
      }
    },
    {
      key: "PI|E|pi|e",
      data: {
        type: types.CONSTANT
      }
    },
    {
      key: "[\\^]",
      data: {
        type: types.OPERATOR,
        args: 2,
        precedence: 3,
        isLeftAssociative: true
      }
    },
    {
      key: "[\\*\\/]",
      data: {
        type: types.OPERATOR,
        args: 2,
        precedence: 2,
        isLeftAssociative: true
      }
    },
    {
      key: "[\\+\\-]",
      data: {
        type: types.OPERATOR,
        args: 2,
        precedence: 1,
        isLeftAssociative: true
      }
    },
    { key: "[(\\[]", data: { type: types.LEFT_PARENTHESIS } },
    { key: "[)\\]]", data: { type: types.RIGHT_PARENTHESIS } },
    { key: "[0-9.,]+", data: { type: types.NUMBER } },
    { key: "[a-zA-Z]", data: { type: types.VARIABLE } }
  ]
};

export default config;

With such a config we'll get the tokens in the form of { type: Operator, value: "^", args: 2, precedence: 3 } .

In order to construct abstract syntax tree out of tokens, we'll use Shunting-yard algorithm by Dijkstra.

import { last } from "./utils";
import {
  isNumber,
  isConstant,
  isVariable,
  isOperator,
  isNamedFunction,
  isLeftParenthesis,
  isRightParenthesis
} from "../queries";

import ASTNode from "./node";

const parse = tokens => {
  const ops = [];
  const nodes = [];

  tokens.forEach(token => {
    // straightforwardly put number / variables / constants in nodes
    if (isNumber(token) || isVariable(token) || isConstant(token)) {
      addOperandNode(nodes, token);
    }

    // push left-parenthesis to ops
    if (isLeftParenthesis(token)) {
      ops.push(token);
    }

    // pull everything out until it's left-parenthesis
    if (isRightParenthesis(token)) {
      while (last(ops) && !isLeftParenthesis(last(ops))) {
        addOperatorNode(nodes, ops.pop());
      }

      ops.pop();
    }

    // pull operators based on precedence & associativity
    if (isOperator(token) || isNamedFunction(token)) {
      while (
        last(ops) &&
        (last(ops).precedence > token.precedence ||
          (token.isLeftAssociative &&
            last(ops).precedence === token.precedence)) &&
        !isLeftParenthesis(token)
      ) {
        addOperatorNode(nodes, ops.pop());
      }

      ops.push(token);
    }
  });

  // if there are still operators in the stack
  while (ops.length > 0) {
    addOperatorNode(nodes, ops.pop());
  }

  return nodes.pop();
};

const addOperandNode = (nodes, token) => {
  const node = new ASTNode(token);

  nodes.push(node);
};

const addOperatorNode = (nodes, token) => {
  const node = new ASTNode(token);

  if (token.args > 1) {
    node.setRight(nodes.pop());
  }
  node.setLeft(nodes.pop());

  nodes.push(node);
};

/*
* :::::::::::::::::::::::::::::::::::::::::::::::::::::::
* :::::::::::::::::::::::: DEMO :::::::::::::::::::::::::
* :::::::::::::::::::::::::::::::::::::::::::::::::::::::
* will omit isLeftAssociative for brevity
*
* parse([
*   { type: NUMBER, value: "2.5" },
*   { type: OPERATOR, value: "+", args: 2, precedence: 1 },
*   { type: NAMED_FUNCTION, value: "sin", args: 1, precedence: 4 },
*   { type: VARIABLE, value: "x" },
*   { type: OPERATOR, value: "^", args: 2, precedence: 3 },
*   { type: NUMBER, value: "3" }
* ])
* ops = [];
* nodes = [];

* -> { type: NUMBER, value: "2.5" }
* ops = []
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" })
* ]

* -> { type: OPERATOR, value: "+", args: 2, precedence: 1 }
* ops = [{ type: OPERATOR, value: "+", args: 2, precedence: 1 }]
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" })
* ]

* -> { type: NAMED_FUNCTION, value: "sin", args: 1, precedence: 4 }
* ops = [
*   { type: OPERATOR, value: "+", args: 2, precedence: 1 },
*   { type: NAMED_FUNCTION, value: "sin", args: 1, precedence: 4 }
* ]
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" })
* ]
*
* -> { type: VARIABLE, value: "x" }
* ops = [
*   { type: OPERATOR, value: "+", args: 2, precedence: 1 },
*   { type: NAMED_FUNCTION, value: "sin", args: 1, precedence: 4 }
* ]
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" }),
*   ASTNode(token: { type: VARIABLE, value: "x" })
* ]
*
* -> { type: OPERATOR, value: "^", args: 2, precedence: 3 }
* ops = [
*   { type: OPERATOR, value: "+", args: 2, precedence: 1 },
*   { type: OPERATOR, value: "^", args: 2, precedence: 3 }
* ]
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" }),
*   ASTNode(
*     token: { type: NAMED_FUNCTION, value: "sin" },
*     left: ASTNode(token: { type: VARIABLE, value: "x" })
*   )
* ]
*
*
* -> { type: NUMBER, value: "3" }
* ops = [
*   { type: OPERATOR, value: "+", args: 2, precedence: 1 },
*   { type: OPERATOR, value: "^", args: 2, precedence: 3 }
* ]
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" }),
*   ASTNode(
*     token: { type: NAMED_FUNCTION, value: "sin" },
*     left: ASTNode(token: { type: VARIABLE, value: "x" })
*   ),
*   ASTNode(token: { type: NUMBER, value: "3" } }),
* ]
*
* -> while (ops.length > 0) block
* ops = [
*   { type: OPERATOR, value: "+", args: 2, precedence: 1 },
* ]
* nodes = [
*   ASTNode(token: { type: NUMBER, value: "2.5" }),
*   ASTNode(
*     token: { type: OPERATOR, value: "^" },
*     left: ASTNode(
*       token: { type: NAMED_FUNCTION, value: "sin" },
*       left: ASTNode(token: { type: VARIABLE, value: "x" })
*     ),
*     right: ASTNode(token: { type: NUMBER, value: "3" } })
*   )
* ]
*
* -> while (ops.length > 0) block
* ops = []
* nodes = [
*   ASTNode(
*     token: { type: OPERATOR, value: "+" },
*     left: ASTNode(token: { type: NUMBER, value: "2.5" }),
*     right: ASTNode(
*       token: { type: OPERATOR, value: "^" },
*       left: ASTNode(
*         token: { type: NAMED_FUNCTION, value: "sin" },
*         left: ASTNode(token: { type: VARIABLE, value: "x" })
*       ),
*       right: ASTNode(token: { type: NUMBER, value: "3" } })
*     )
*   )
* ]
*/

That's it. You can look at actual code on Github. Hope you find this article helpful.