Math AST: Tokenizer in JavaScript

Tokenizer splits string or text (in this case math expression) into the tokens - the smallest possible building blocks. Numbers, variables, constants, operators, functions, parenthesis, etc. Atoms in the mathematical world. Take a look at this picture for a quick demonstration.

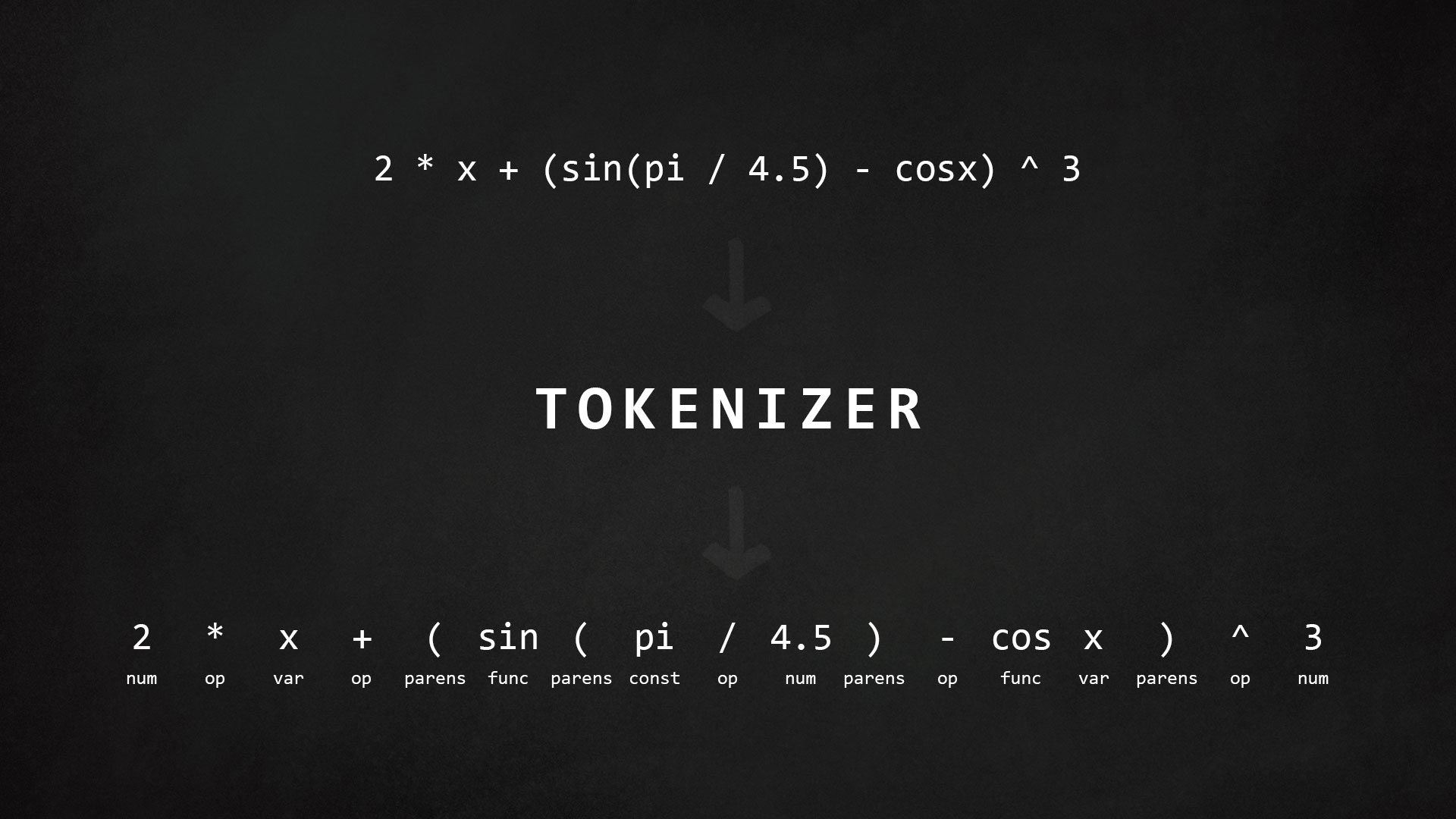
We are going to build simple math tokenizer in JavaScript. Simple, because we will restrict ourselves with basic math operators & functions, for the sake of brevity.

First of all we need to define what are we going to consider as token. Analyzing this will give us a rough idea of how exactly we should split math expression.

• Numbers: 1, 44, 3.48, 0.99. Integers & floats, single or multiple digits. At this stage it's already clear that splitting string into single characters & checking them one by one won't be really convenient. RegExp seems like an easier solution.
• Variables: x, y, ..., z, X, Y. Alphabetical characters. Single or multiple characters though? In math expressions like ab + 2 are we considering ab as implicit multiplication of two variables or one variable? Personally I'd prefer the former, but the latter is easier, so we will take that option.
• Functions: sin, cos, tg, ctg, .... But if we are considering multiple alphabetical characters as variables, how are we going to catch functions? Looks like we need to catch them in reverse order - functions first, then variables.
• Constants: pi, e, PI, E. Have the same problem as functions, hence have the same solution. Functions, constants, variables. We will catch them in that order.
• Parenthesis: (, [, ], ).
• Operators: +, -, *, /, ^.

Ideally, I'd like to pass the ordered list of rules in the form of { key: RegExp, type } and receive array of tokens in the form of { type, value }.

import types from "./types";

const config = {
  rules: [
    {
      key: "sin|cos|tg|ctg|log|sqrt",
      data: {
        type: types.NAMED_FUNCTION
      }
    },
    {
      key: "PI|E|pi|e",
      data: {
        type: types.CONSTANT
      }
    },
    {
      key: "[\\+\\-\\*\\/\\^]",
      data: {
        type: types.OPERATOR
      }
    },
    { key: "[(\\[]", data: { type: types.LEFT_PARENTHESIS } },
    { key: "[)\\]]", data: { type: types.RIGHT_PARENTHESIS } },
    { key: "[0-9.,]+", data: { type: types.NUMBER } },
    { key: "[a-zA-Z]+", data: { type: types.VARIABLE } }
  ]
};

export default config;

Now, that preparations are done, it's time to get hands dirty. In a nutshell the idea is to split string using rule's key into array and replace matched substring with token. Continue until we run out of rules. We will have to deal with whitespaces, so implicitly we will add additional rule { key: ".+", type: Unknown } to get rid of them.

import { getRules, isUnknown, zipConcat, buildToken } from "./utils";

function tokenize(config, expression) {
  // add UNKNOWN_RULE to remove whitespaces & turn keys into RegExp
  const rules = getRules(config);

  // wrap for convenience
  const targets = [expression];

  let output;

  // run every rule on targets
  output = rules.reduce(applyRuleOnTargets, targets);

  // remove tokens with type: Unknown
  output = output.reject(isUnknown);

  return output;
}

function applyRuleOnTargets(targets, rule) {
  let output;

  // run every rule on target
  output = targets.map(target => applyRuleOnTarget(target, rule));

  // flatten one level deep ["a", "b", ["c"]] -> ["a", "b", "c"]
  output = flatten(output);

  // clear from empty-ish values ["a", "", "b", null, "c"] -> ["a", "b", "c"]
  output = compact(output);

  return output;
}

function applyRuleOnTarget(target, rule) {
  // no need to do anything if it's not a string
  if (isToken(target)) {
    return target;
  }

  // splits string into array of substrings
  const split = target.split(rule.key);

  // find matched substrings and produce tokens out of them
  const match = target.match(rule.key).map(buildToken(rule.data));

  // sequentally concatenate arrays: zipConcat([a1, a2], [b1, b2]) -> [a1, b1, a2, b2]
  return zipConcat(split, match);
}

/*
* :::::::::::::::::::::::::::::::::::::::::::::::::::::::
* :::::::::::::::::::::::: DEMO :::::::::::::::::::::::::
* :::::::::::::::::::::::::::::::::::::::::::::::::::::::
* tokenize(config, "2.5 + sinx^3")
*
* -> NAMED_FUNCTION_RULE
* [
*   "2,5 + ",
*   { type: NAMED_FUNCTION, value: "sin" },
*   "x^3"
* ]
*
* -> OPERATOR_RULE
* [
*   "2,5 ",
*   { type: OPERATOR, value: "+" },
*   " ",
*   { type: NAMED_FUNCTION, value: "sin" },
*   "x"
*   { type: OPERATOR, value: "^" },
*   "3"
* ]
*
* -> NUMBER_RULE
* [
*   { type: NUMBER, value: "2.5" },
*   " ",
*   { type: OPERATOR, value: "+" },
*   " ",
*   { type: NAMED_FUNCTION, value: "sin" },
*   "x"
*   { type: OPERATOR, value: "^" },
*   { type: NUMBER, value: "3" }
* ]
*
* -> VARIABLE_RULE
* [
*   { type: NUMBER, value: "2.5" },
*   " ",
*   { type: OPERATOR, value: "+" },
*   " ",
*   { type: NAMED_FUNCTION, value: "sin" },
*   { type: VARIABLE, value: "x" },
*   { type: OPERATOR, value: "^" },
*   { type: NUMBER, value: "3" }
* ]
*
* -> UNKNOWN_RULE
* [
*   { type: NUMBER, value: "2.5" },
*   { type: UNKNOWN, value: " " },
*   { type: OPERATOR, value: "+" },
*   { type: UNKNOWN, value: " " },
*   { type: NAMED_FUNCTION, value: "sin" },
*   { type: VARIABLE, value: "x" },
*   { type: OPERATOR, value: "^" },
*   { type: NUMBER, value: "3" }
* ]
*
* -> reject(isUnknown)
* [
*   { type: NUMBER, value: "2.5" },
*   { type: OPERATOR, value: "+" },
*   { type: NAMED_FUNCTION, value: "sin" },
*   { type: VARIABLE, value: "x" },
*   { type: OPERATOR, value: "^" },
*   { type: NUMBER, value: "3" }
* ]
*
*/

That's it. You can look at actual code on Github. Hope you find this article helpful. Next on the agenda - constructing abstract syntax tree (AST) out of tokens.